进制与位运算详解
进制
计数进位的方法称为进制(Numeration System)。常见的进制有以下几种。
十进制(Decimal System)
我们日常使用的计数系统,基数为 10,数位可以是 0 到 9。
二进制(Binary System)
计算机内部使用的计数系统,基数为 2,数位只能是 0 或 1。
八进制(Octal System)
基数为 8,数位为 0 到 7。
十六进制(Hexadecimal System)
基数为 16,数位为 0 到 9 以及字母 A 到 F,常用于表示内存地址、颜色值等。
进制的基数与位权
在进制系统中,有两个重要的概念:基数和位权。
基数
基数是进制的基本数。例如:
- 二进制的基数是 2。
- 八进制的基数是 8。
- 十进制的基数是 10。
- 十六进制的基数是 16。
位权
位权是指数位在数值中的权重,决定了该位对整个数值的影响。位权通常是基数的幂次方。
例如,在十进制数 123 中,各位的位权为:
- 最右边的 3,位权为 100。
- 中间的 2,位权为 101。
- 最左边的 1,位权为 102。
在二进制中,同样适用,位权为 2 的幂。
原码、反码与补码
计算机的运算器通常只执行加法,没有直接的减法运算。因此,减法通过加上一个数的相反数来实现。
乘法和除法也可以通过位移操作来优化:
- 乘法:左移操作,数值每左移一位,相当于乘以 2。
- 除法:右移操作,数值每右移一位,相当于除以 2。
符号位
在二进制表示有符号数时,最高位通常作为符号位:
- 符号位为 0,表示正数。
- 符号位为 1,表示负数。
原码、反码和补码的表示
原码
原码是数字的二进制表示形式,直接用最高位表示符号位,其余位表示数值的绝对值。
反码
正数的反码与原码相同。负数的反码是对其原码除符号位外的各个位取反。
补码
正数的补码与原码相同。负数的补码是在其反码的基础上加 1。
示例
以 8 位二进制数表示+6 和-6:
-
+6 的原码:
0000 0110 -
+6 的反码:
0000 0110 -
+6 的补码:
0000 0110 -
-6 的原码:
1000 0110 -
-6 的反码:
1111 1001(符号位不变,其他位取反) -
-6 的补码:
1111 1010(反码加 1)
为什么要有反码和补码
使用补码有以下原因:
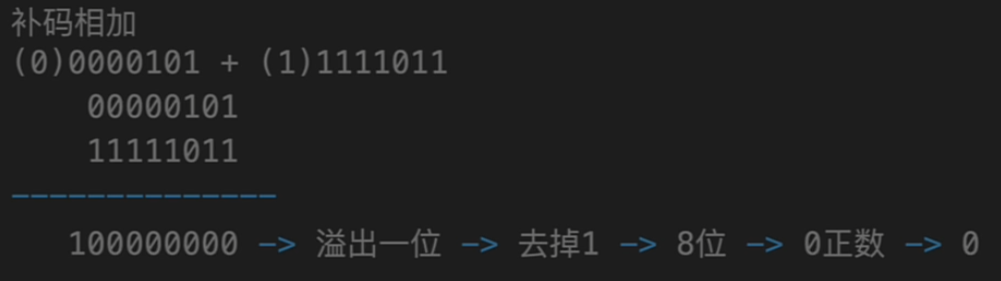
- 统一运算:补码可以将减法运算转换为加法运算,简化了计算机的电路设计。
- 唯一的零表示:补码表示中,零只有一种形式,避免了正零和负零的区别。
- 便于溢出检测:补码运算有助于检测溢出错误。
计算机的内存中,整数通常以补码的形式存储。
位运算
位运算是直接对整数的二进制位进行操作。由于直接操作二进制位,位运算的性能非常高。
按位与 & 和按位或 |
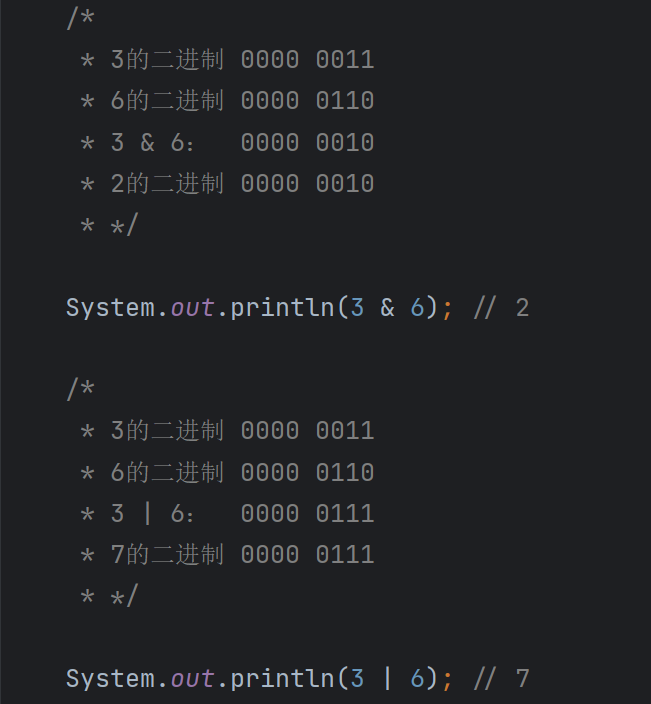
- 按位与
&:两个二进制数对应位都为 1,结果才为 1,否则为 0。 - 按位或
|:两个二进制数对应位只要有一个为 1,结果为 1,只有当对应位都为 0 时,结果才为 0。
按位取反 ~ 和异或 ^
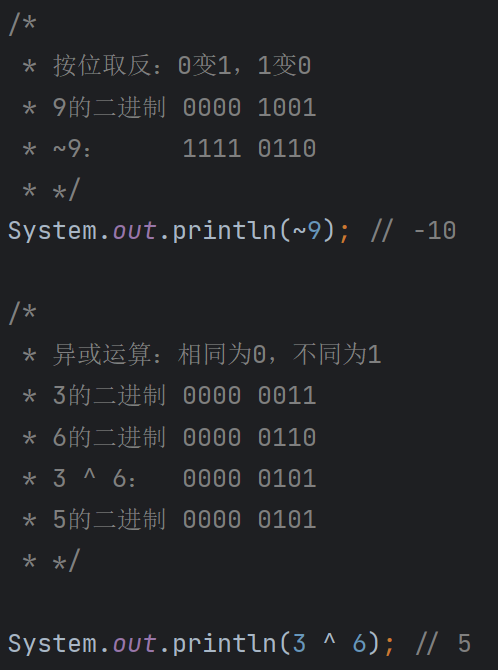
- 按位取反
~:对二进制数的每一位取反,0 变 1,1 变 0。 - 异或
^:两个二进制数对应位相同为 0,不同为 1。
位移运算符
-
左移运算符
<<将二进制数的所有位向左移动指定的位数,右边补 0。每左移一位,相当于乘以 2。
-
右移运算符
>>将二进制数的所有位向右移动指定的位数,左边补符号位。每右移一位,相当于除以 2。
-
无符号右移运算符
>>>将二进制数的所有位向右移动指定的位数,左边补 0,不论符号位。
示例
假设有整数 8,其二进制表示为 00001000:
8 << 1结果为16,二进制为00010000。8 >> 1结果为4,二进制为00000100。-8 >> 1结果为-4,符号位保持不变,左边补 1。-8 >>> 1结果为一个较大的正整数,因为左边补 0,符号位被当作数值位。
注意事项
- 位运算只能用于整数类型,如
byte、short、int、long和char。 - 在处理有符号数的位移时,需要注意符号位的影响。